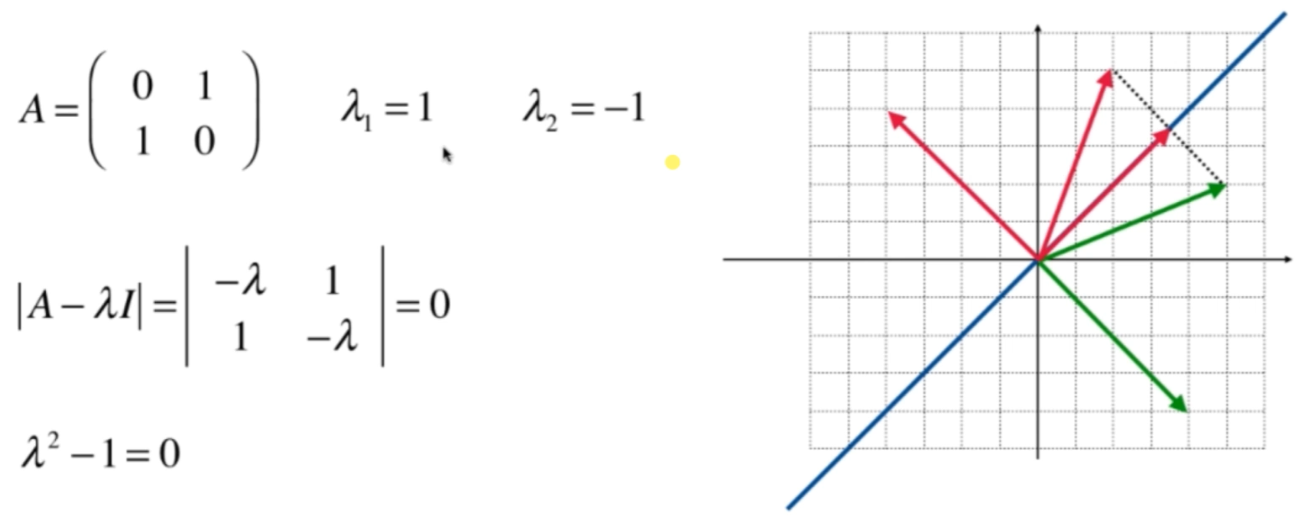<< 返回 Menu

import numpy as np
from numpy.linalg import eig

A1=np.array([[4,-2],[1,1]])
eigenvalues1, eigenvectors1 = eig(A1)
print(eigenvalues1)
print(eigenvectors1)
print()

# 关于 y=x 翻转
A2=np.array([[0,1],[1,0]])
eigenvalues2, eigenvectors2 = eig(A2)
print(eigenvalues2)
print(eigenvectors2)
print()

# 旋转90度
A3=np.array([[0,-1],[1,0]])
eigenvalues3, eigenvectors3 = eig(A3)
print(eigenvalues3)
print(eigenvectors3)
print()

# 单位矩阵
A4=np.array([[1,0],[0,1]])
eigenvalues4, eigenvectors4 = eig(A4)
print(eigenvalues4)
print(eigenvectors4)
print()

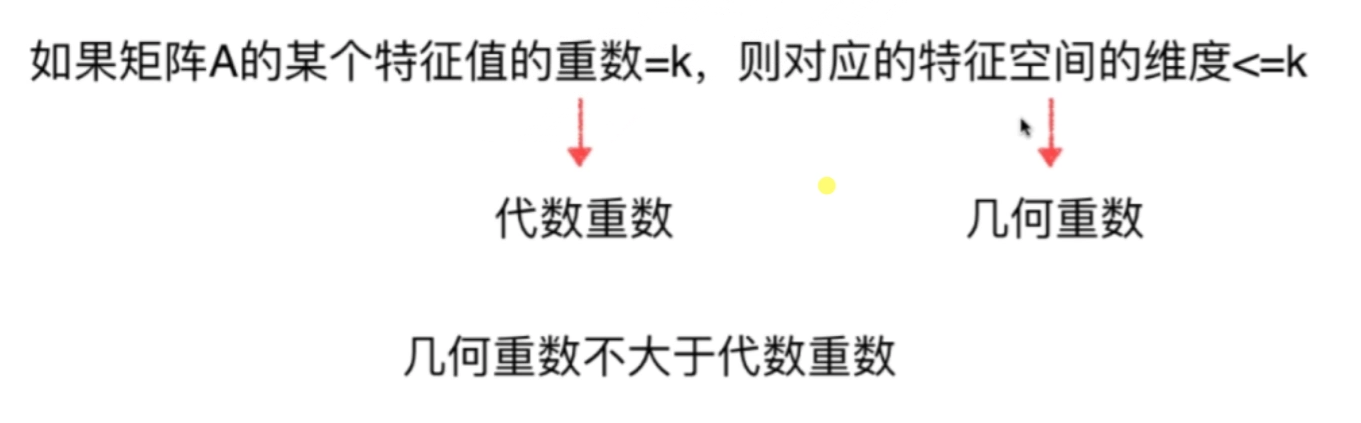
# 代数重数为2但几何重数为1
A5=np.array([[3,1],[0,3]])
eigenvalues5, eigenvectors5 = eig(A5)
print(eigenvalues5)
print(eigenvectors5)
print()

[3. 2.]
[[0.89442719 0.70710678]
 [0.4472136  0.70710678]]

[ 1. -1.]
[[ 0.70710678 -0.70710678]
 [ 0.70710678  0.70710678]]

[0.+1.j 0.-1.j]
[[0.70710678+0.j         0.70710678-0.j        ]
 [0.        -0.70710678j 0.        +0.70710678j]]

[1. 1.]
[[1. 0.]
 [0. 1.]]

[3. 3.]
[[ 1.00000000e+00 -1.00000000e+00]
 [ 0.00000000e+00  6.66133815e-16]]

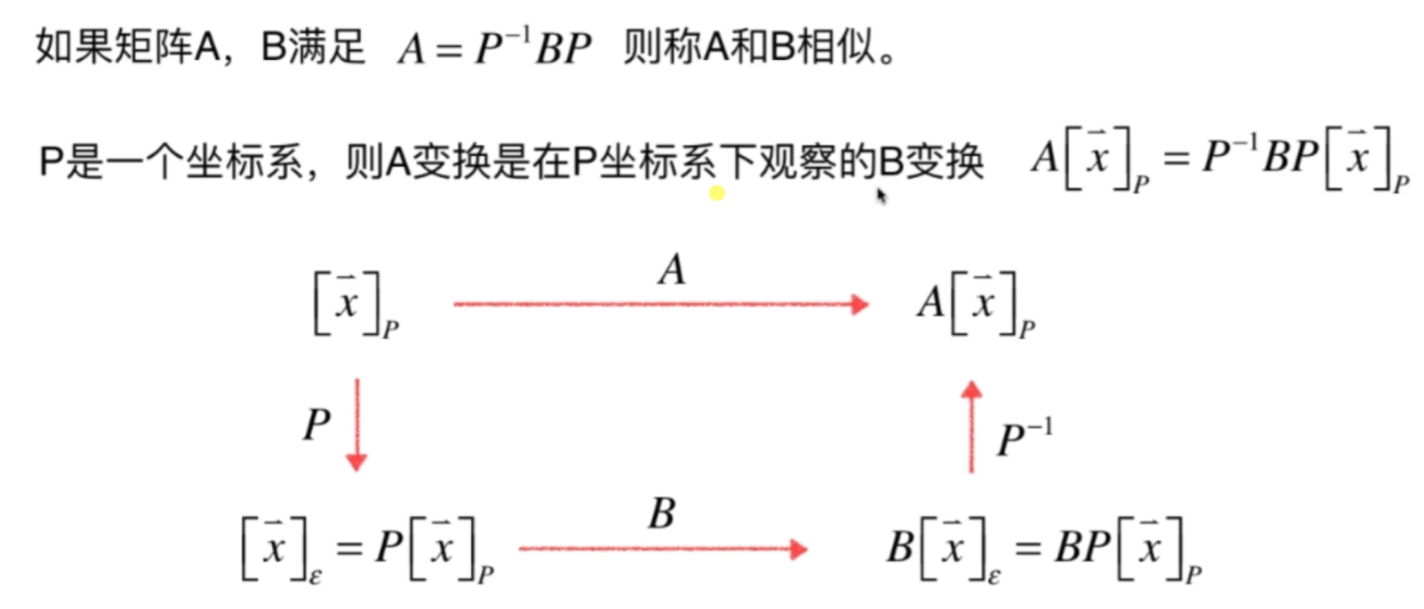
### 矩阵对角化

import numpy as np
from numpy.linalg import eig, inv
from numpy.linalg import matrix_rank
# 或者用自己写的 rank()

def diagonalize(A):
    
    assert A.ndim == 2
    assert A.shape[0] ==A.shape[1]
    
    eigenvalues, eigenvectors = eig(A)
    
    P = eigenvectors
    if matrix_rank(np.array(P.tolist())) != A.shape[0]:
        print("Matrix can not be diagonalized!")
        return None, None, None
                   
    D = np.diag(eigenvalues)
    Pinv = inv(P)
    
    return P, D, Pinv


A1 = np.array([[4,-2],[1,1]])
P1, D1, Pinv1 = diagonalize(A1)
print(P1)
print(D1)
print(Pinv1)
print(P1.dot(D1).dot(Pinv1))
print()


A2 = np.array([[3,1],[0,3]])
P2, D2, Pinv2 = diagonalize(A2)
print(P2)
print(D2)
print(Pinv2)
print()

[[0.89442719 0.70710678]
 [0.4472136  0.70710678]]
[[3. 0.]
 [0. 2.]]
[[ 2.23606798 -2.23606798]
 [-1.41421356  2.82842712]]
[[ 4. -2.]
 [ 1.  1.]]

Matrix can not be diagonalized!
None
None
None