<< 返回 Menu

坐标转换

在n维空间，如果给定一组基，任何一个向量（或者是点）都可以表示成这组基的线性组合，且表示方法唯一。

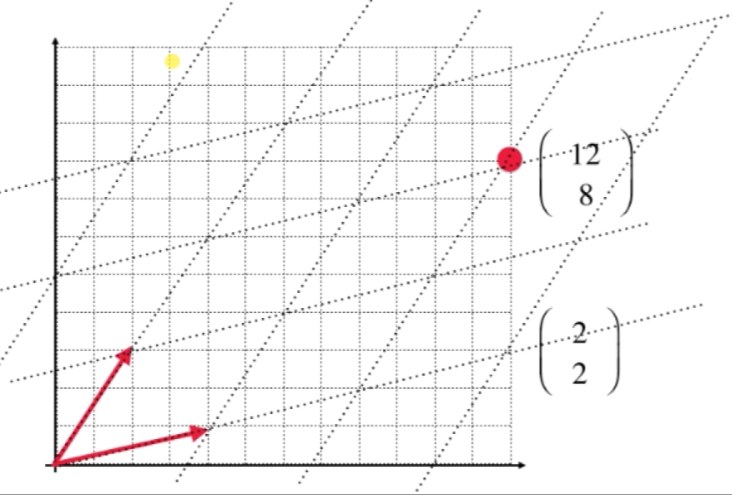
$\begin{pmatrix} 12 \\ 8 \end{pmatrix}$ 对 $\vec{e_1}=\begin{pmatrix} 1 & 0 \end{pmatrix}^T \quad \vec{e_2}=\begin{pmatrix} 0 & 1 \end{pmatrix}^T$ 来说：$\begin{pmatrix} 12 & 8 \end{pmatrix}^T = 12 \begin{pmatrix} 1 & 0 \end{pmatrix}^T + 8 \begin{pmatrix} 0 & 1 \end{pmatrix}^T = 12 \vec{e_1} + 8 \vec{e_2}$
对 $\vec{u}=\begin{pmatrix} 4 & 1 \end{pmatrix}^T \quad \vec{v}=\begin{pmatrix} 2 & 3 \end{pmatrix}^T$ 来说：$\begin{pmatrix} 12 & 8 \end{pmatrix}^T = 2 \begin{pmatrix} 4 & 1 \end{pmatrix}^T + 2 \begin{pmatrix} 2 & 3 \end{pmatrix}^T = 2 \vec{u} + 2 \vec{v}$

$\epsilon = \left\{ \vec{e_1} \quad \vec{e_2} \right\}$ 标准基（Standard Basis） 标准坐标系

n维标准基（n维标准坐标系）$\epsilon = \left\{ \vec{e_1} \quad \vec{e_2} \quad \vec{e_3} \quad ... \quad \vec{e_n}\right\}$

假设有一组基：$B = \left\{ \vec{b_1}, \vec{b_2}, \vec{b_3}, ..., \vec{b_n}\right\}$ 设立矩阵 $P_B = \begin{pmatrix} \vec{b_1} \quad \vec{b_2} \quad \vec{b_3} \quad ... \quad \vec{b_n}\end{pmatrix}$ (坐标转换矩阵)，在这组基下的一个向量 $[\vec{x}]$
有： $[\vec{x}]_\epsilon = P_B[\vec{x}]_B \quad P_B[\vec{x}]_B = P_B^{-1}[\vec{x}]_\epsilon$

假设有一组基：$B = \left\{ \vec{b_1}, \vec{b_2}, \vec{b_3}, ..., \vec{b_n}\right\} \quad$ 另一组基：$C = \left\{ \vec{c_1}, \vec{c_2}, \vec{c_3}, ..., \vec{c_n}\right\}$
已知在B这组基下的一个向量 $[\vec{x}]_B$，求：$[\vec{x}]_C$
$[\vec{x}]_C = P_C^{-1}P_B[\vec{x}]_B \quad [\vec{x}]_C = P_{B \rightarrow C}[\vec{x}]_B \quad P_{B \rightarrow C} = P_C^{-1}P_B$

线性变换

变换是一个函数

一个变换$T(x)$称为线性变化，必须满足：
$T(u+v) = T(u) + T(v)$
$T(cu)=cT(u) \quad c \in R$
所有的矩阵都可以用来表示一个线性变换
用矩阵表示空间的视角和用矩阵表示变换的视角是等价的