标准正交矩阵¶
一组n维标准正交基 $\vec{v_1},\vec{v_2},\vec{v_3},...,\vec{v_n}$ 按照列的方式排成一个n阶方阵$Q$,称$Q$为标准正交矩阵
标准正交矩阵的重要性质:
- $Q^T \cdot Q = I$
- $Q$的各列线性无关
- $Q$可逆
- $Q^T$是$Q$的左逆
- $Q^T$是$Q$的右逆
- $Q^T$是$Q$的逆
- $Q^{-1}=Q^T$
矩阵的QR分解¶
$A=QR \longrightarrow R=Q^{-1}A \longrightarrow R=Q^T A$
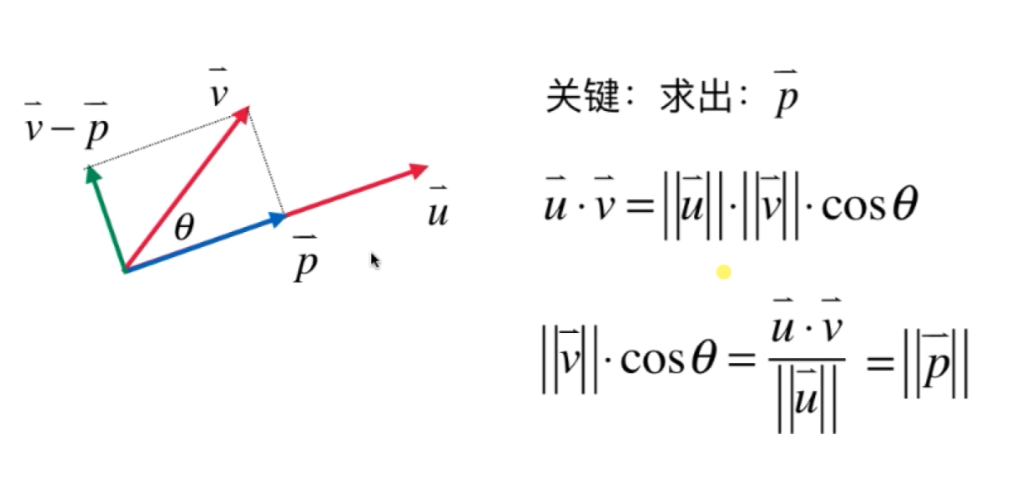
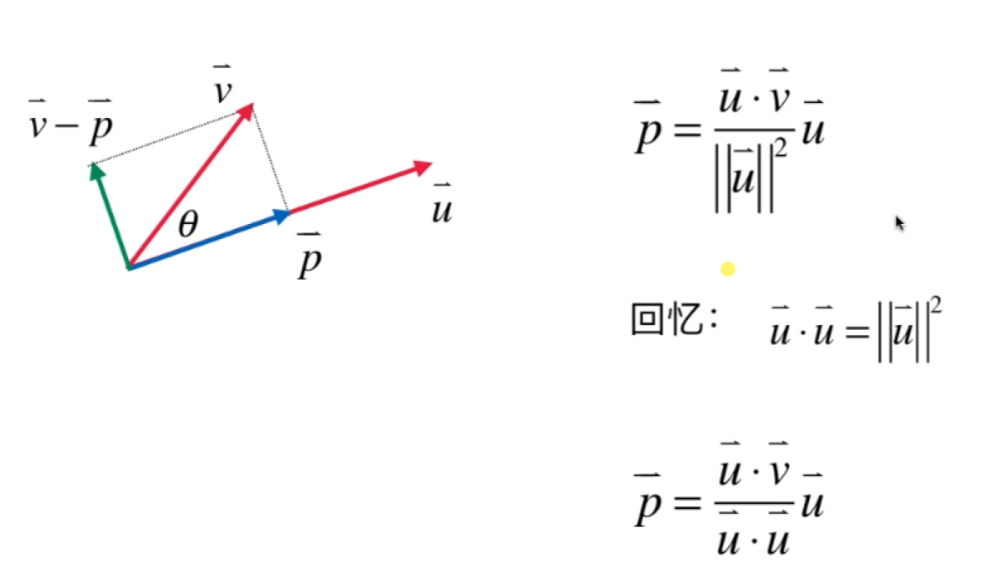 因为是向量运算因此$\vec{u}$是不能做约分的
因为是向量运算因此$\vec{u}$是不能做约分的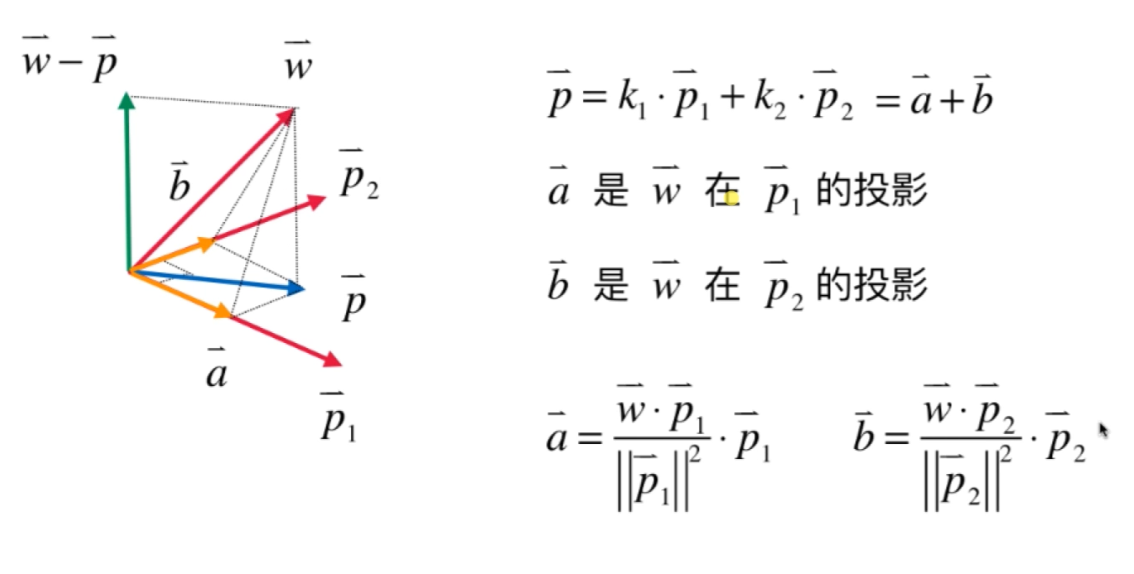
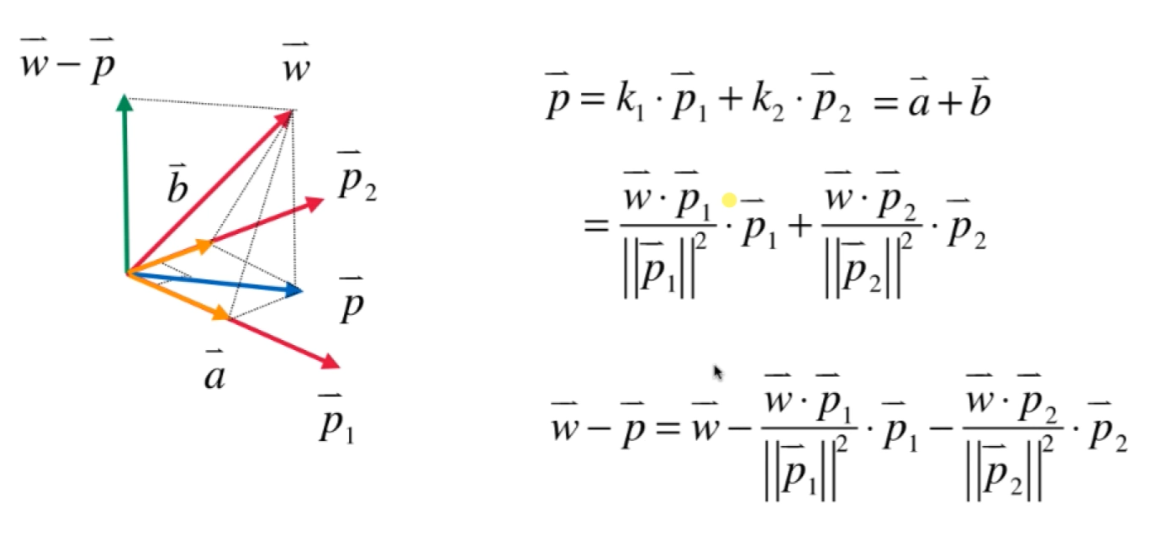
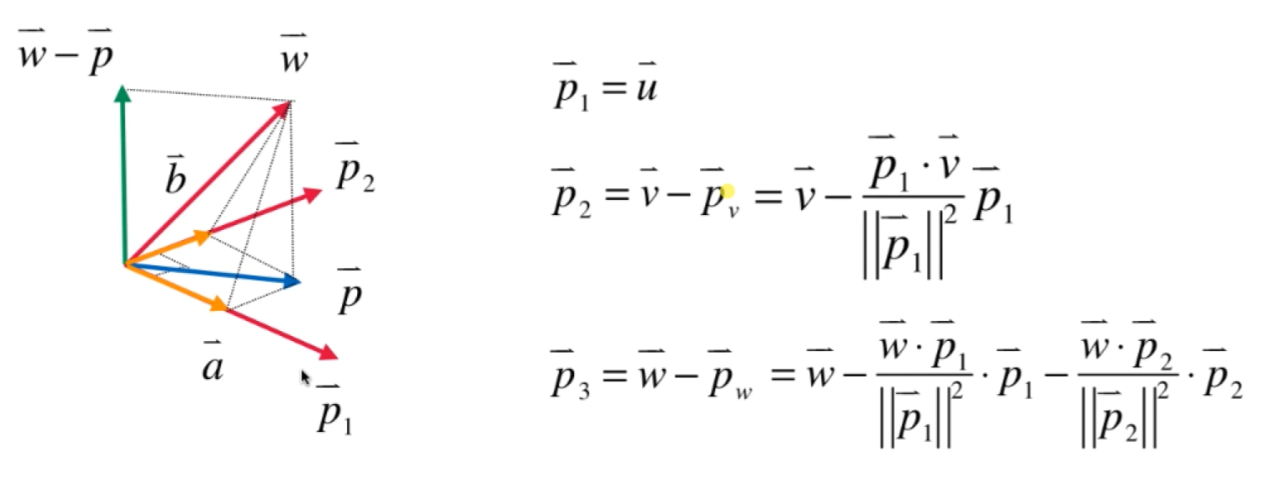
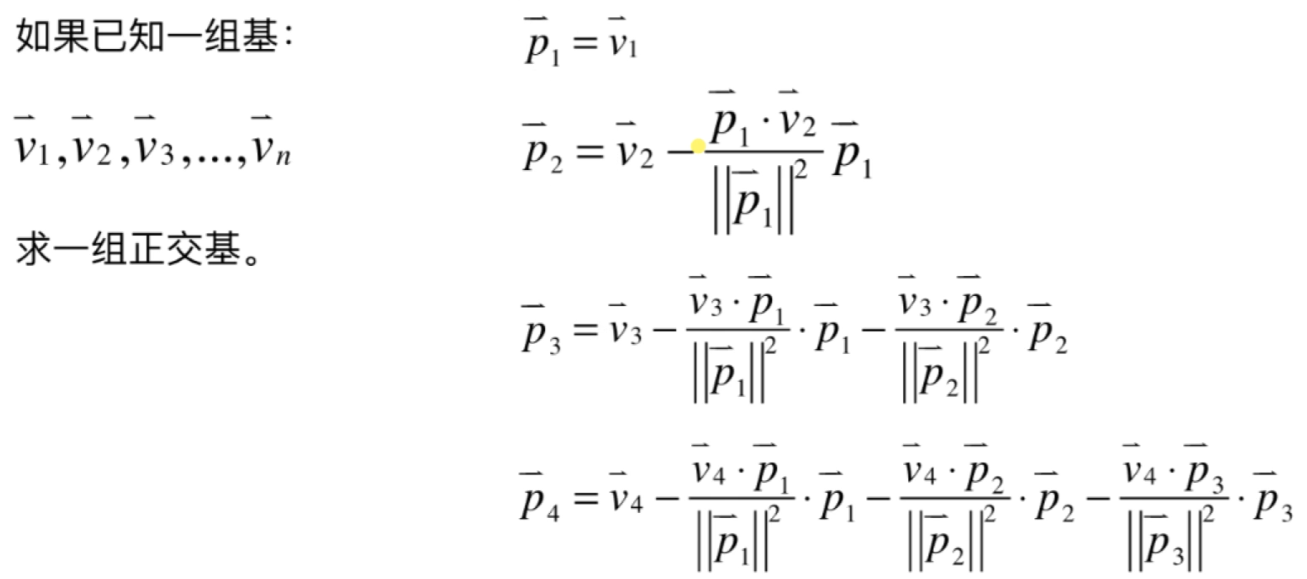 此为 Gram-Schmidt 过程(注意,算法的输入是一组基,即线性无关的)
此为 Gram-Schmidt 过程(注意,算法的输入是一组基,即线性无关的)