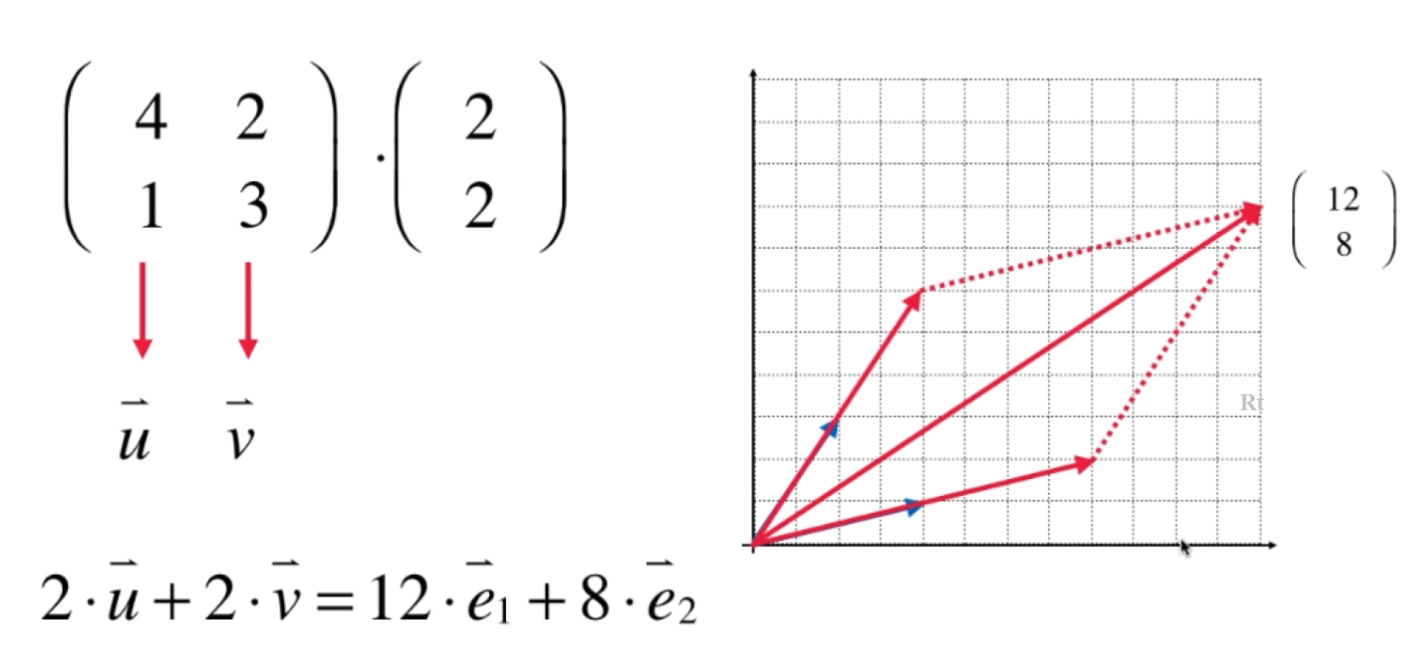线性组合¶
向量的两个最基本的运算:向量加法 $\vec{v} + \vec{w}$ 和 标量乘法 $k \vec{v}$,构建了线性代数中最重要的一个概念:线性组合
对于若干个n维向量 $\vec{v_1}, \vec{v_2}, \vec{v_3}, ... \vec{v_p}$
$k_1 \cdot \vec{v_1} + k_2 \cdot \vec{v_2} + k_3 \cdot \vec{v_3} + ... + k_p \cdot \vec{v_p}$ 称为这些向量的一个线性组合
对于若干个n维向量 $\vec{v_1}, \vec{v_2}, \vec{v_3}, ... \vec{v_p}$ 存在一组k不全为0,使得 $k_1 \cdot \vec{v_1} + k_2 \cdot \vec{v_2} + k_3 \cdot \vec{v_3} + ... + k_p \cdot \vec{v_p}=0$,则称$\vec{v_1}, \vec{v_2}, \vec{v_3}, ... \vec{v_p}$线性相关;只有k全部为0时,才有$\vec{v_1}, \vec{v_2}, \vec{v_3}, ... \vec{v_p}$线性无关,则任何一个向量都不可以表示成其他向量的线性组合。
如果$\vec{v_1}, \vec{v_2}, \vec{v_3}, ... \vec{v_n}$ 线性相关 $\Longleftrightarrow$ 其中一个向量(k不为零的)可以写成其他向量的线性组合
如果$\vec{v_1}, \vec{v_2}, \vec{v_3}, ... \vec{v_n}$ 线性无关 $\Longleftrightarrow$ 没有一个向量可以写成其他向量的线性组合
m个n维向量$\vec{v_1}, \vec{v_2}, \vec{v_3}, ... \vec{v_m}$,若m>m,则$\vec{v_1}, \vec{v_2}, \vec{v_3}, ... \vec{v_m}$线性相关
- 100个三维向量一定线性相关
- 4个三维向量一定线性相关
- 3个三维向量就不一定了
在二维平面中,两个向量不共线,则这两个向量线性无关;
在三维空间中,三个向量不共面,则这三个向量线性无关;
生成空间¶
对于一个n维空间,至少需要n个向量才能够生成。
空间的基¶
若m个向量生成n维空间,m最小为n;若m个n维向量线性无关,m最大为n;若一组向量可以生成整个n维空间,且线性无关,这组向量一定有n个,则称这组向量为n维空间的一组基。
n个n维向量 $\vec{v_1}, \vec{v_2}, \vec{v_3}, ... \vec{v_n}$,若他们是这个n维空间的基 $\Longleftrightarrow$
- $\vec{v_1}, \vec{v_2}, \vec{v_3}, ... \vec{v_n}$ 生成整个n维空间
- $\vec{v_1}, \vec{v_2}, \vec{v_3}, ... \vec{v_n}$ 线性无关
在n维空间,如果给定一组基,任何一个向量(或者是点)都可以表示成这组基的线性组合,且表示方法唯一。
矩阵表示空间¶
理解为新的坐标系